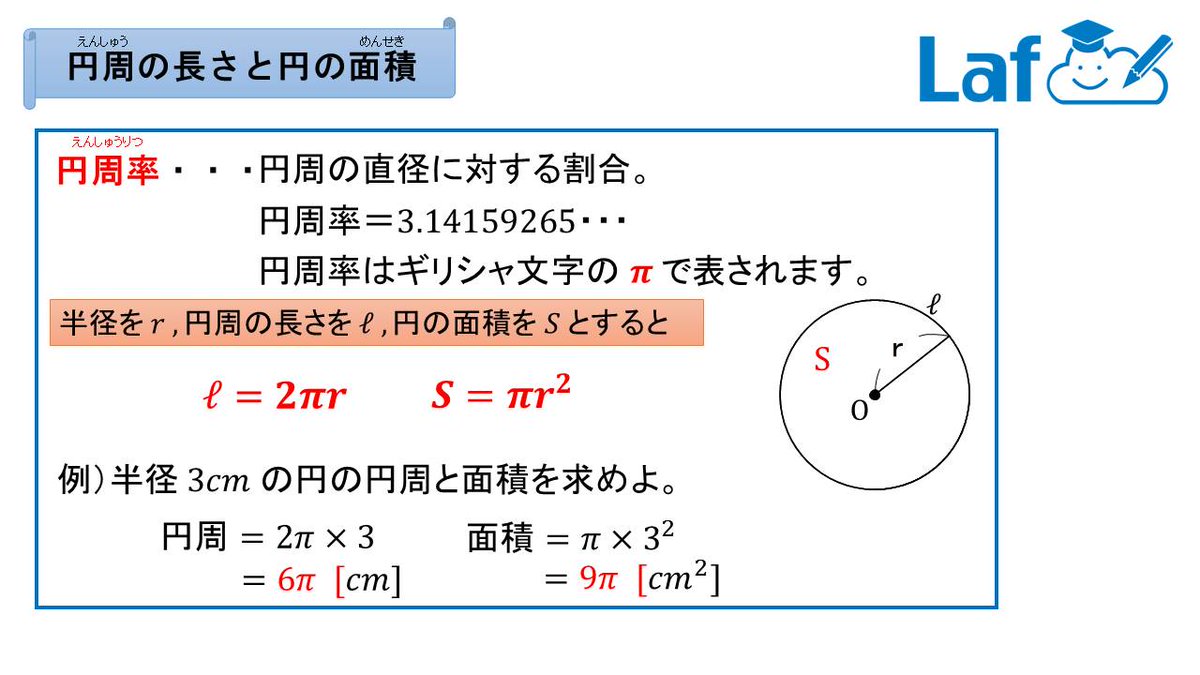
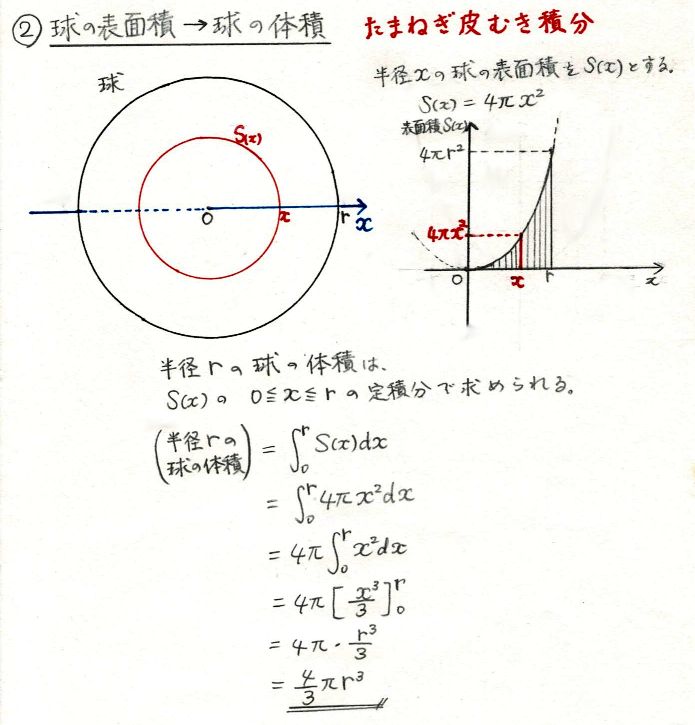
Web 円の面積、球の体積の公式の微積による証明(導出) そもそもこれは微積を用いないと厳密には証明できない感じです。 球の体積公式 まずは公式を書いておきます。 半径
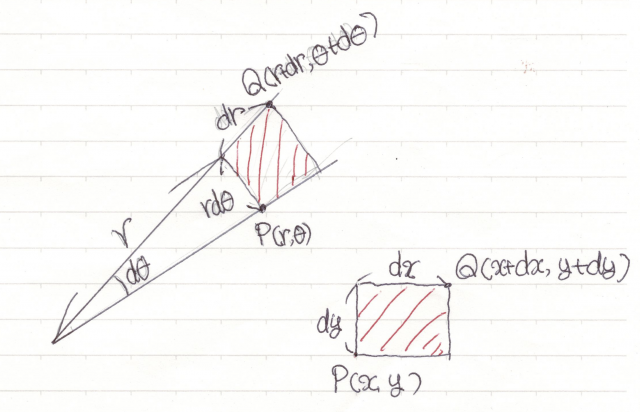
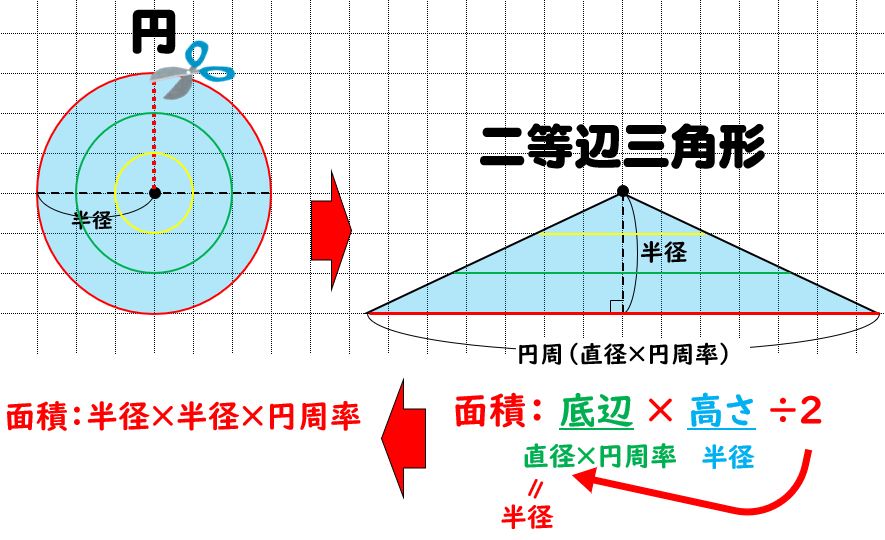
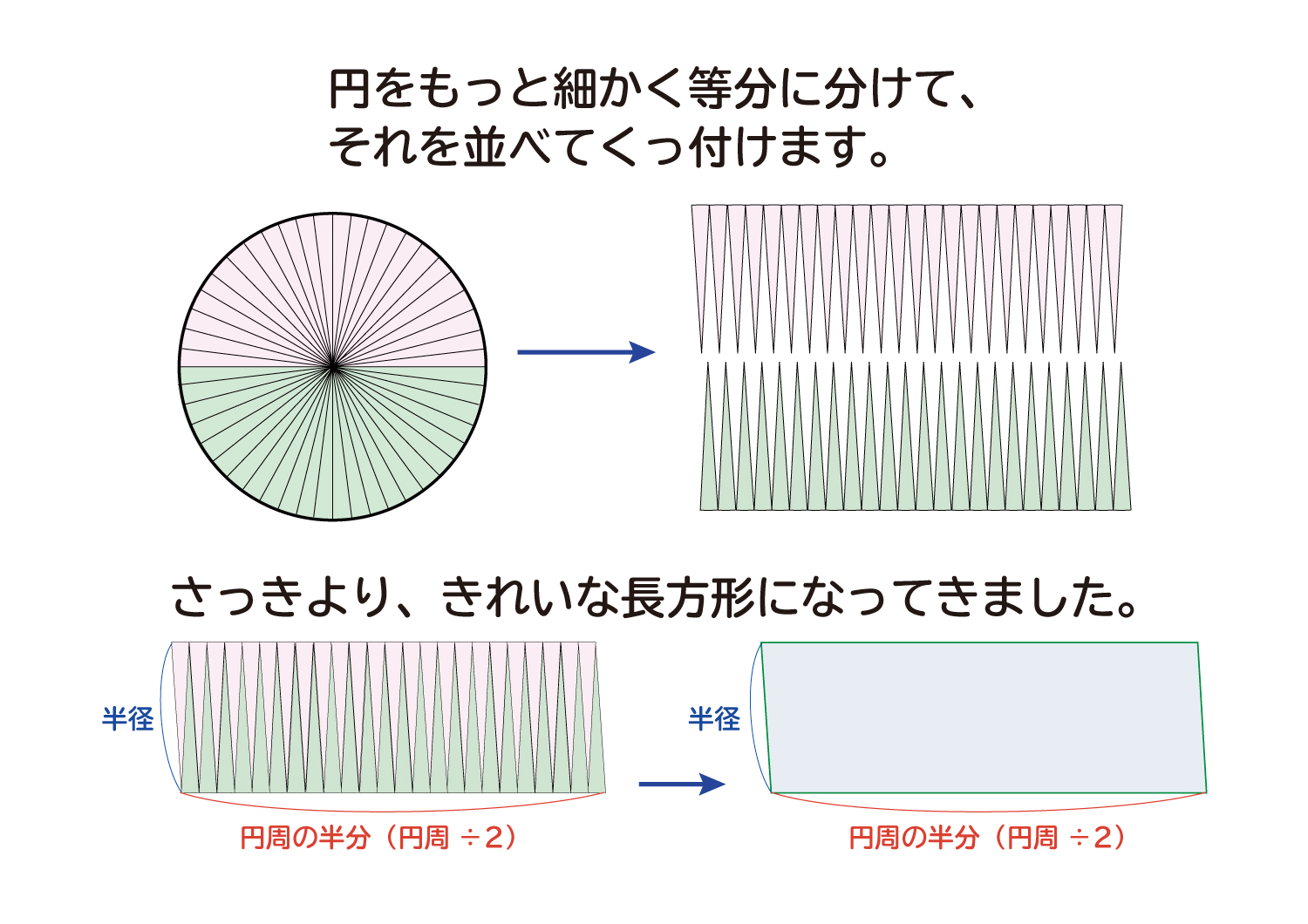
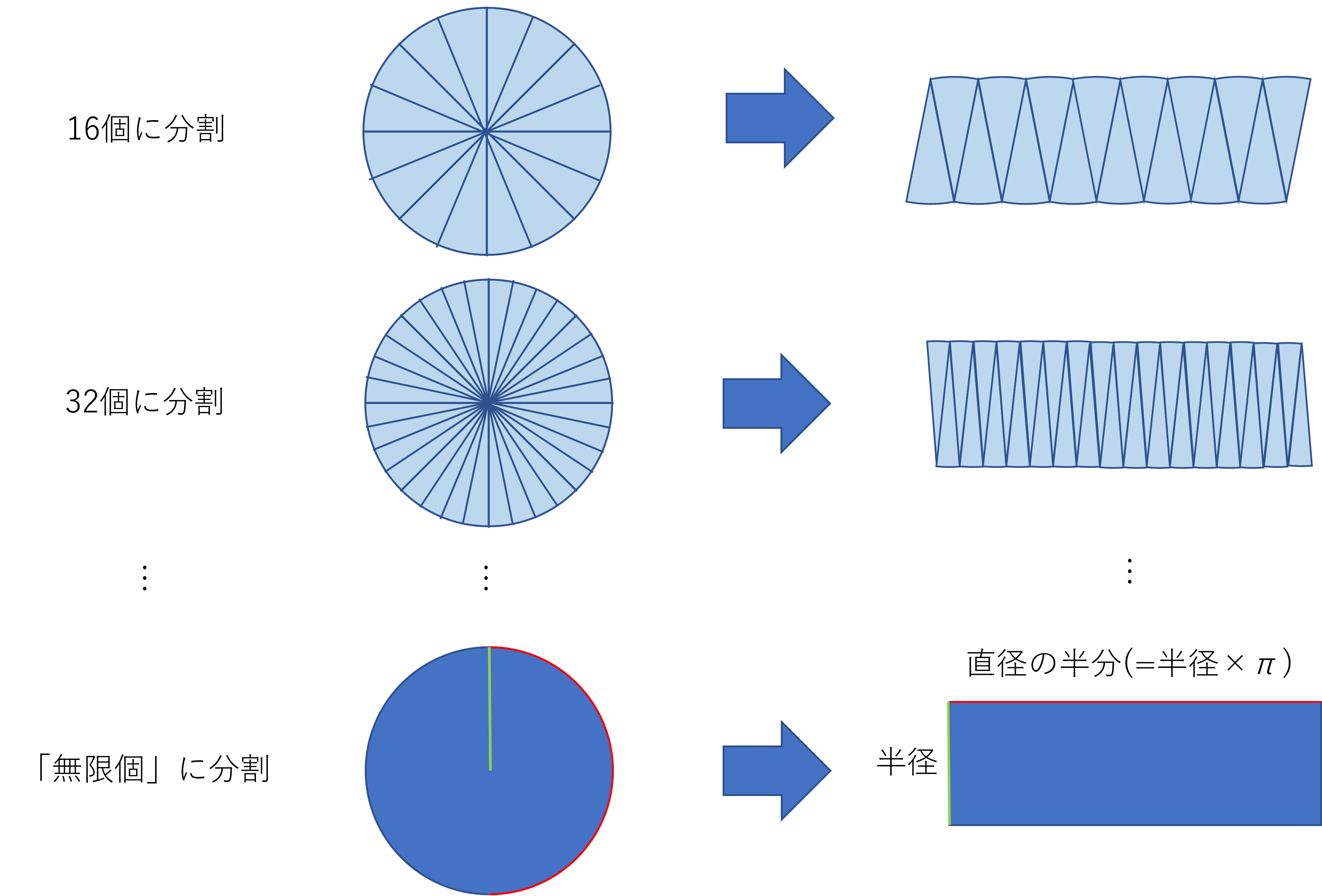
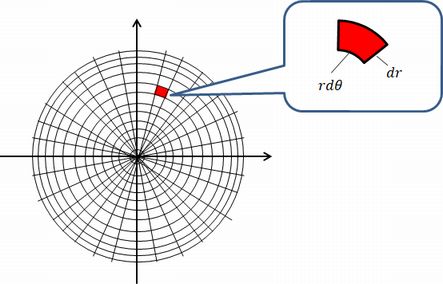
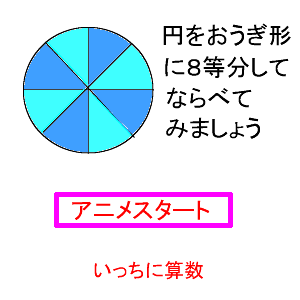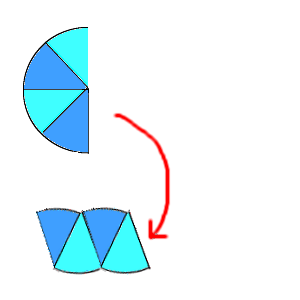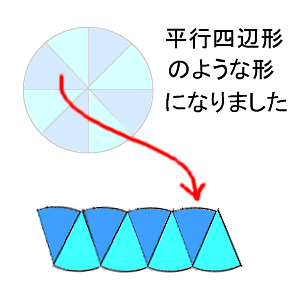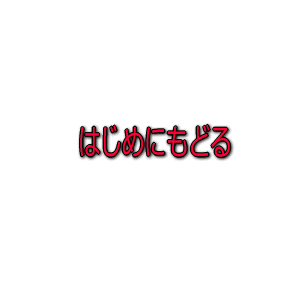
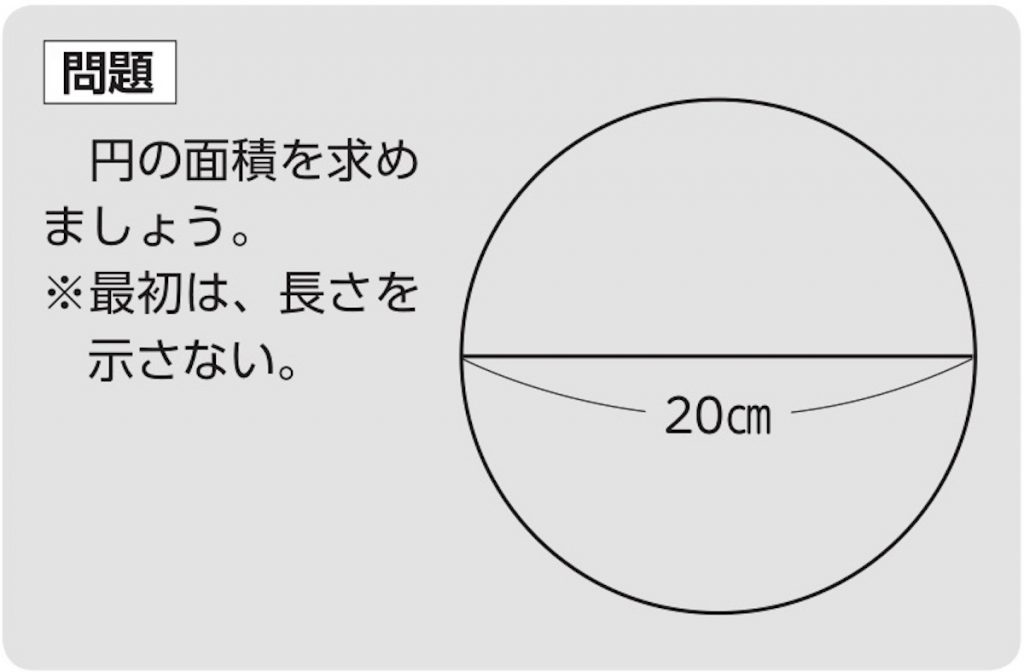
円 面積 積分 一部-Web平行四辺形の面積(2辺と夾角から) 円に内接する四角形の面積(4辺から) 四角形の面積(4辺と対角の和から) 正多角形の面積 正多角形の面積から辺 円の面積 円の面積から半径 扇形Web 同様の考え方により,平面上の任意の面積 S が,微小な面積 Δ S i を用いて (3) ∑ i = 1 N Δ S i とし,分割数を無限にする極限により (4) S = lim N → ∞ ∑ i = 1 N Δ S i = ∫ S d
円 面積 積分 一部のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 |  |  |
 |  | |
 |  |  |
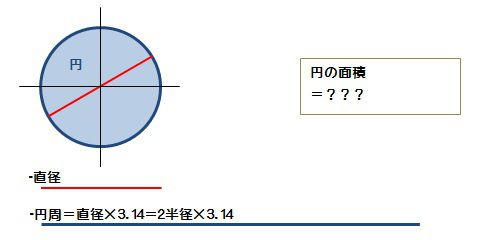 | 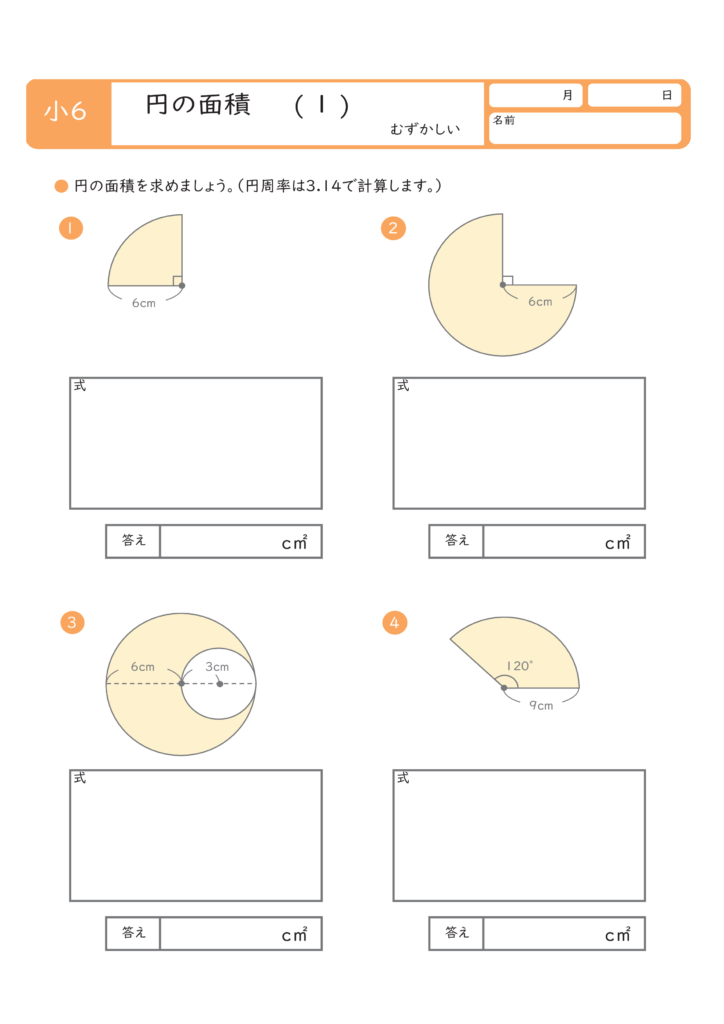 | |
「円 面積 積分 一部」の画像ギャラリー、詳細は各画像をクリックしてください。
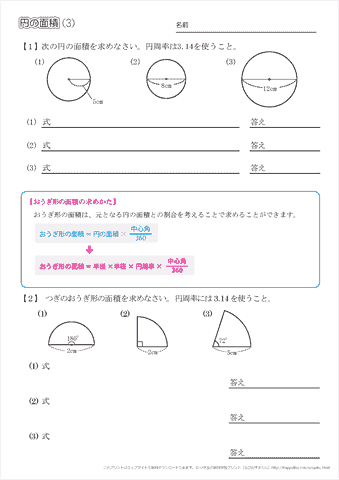 | 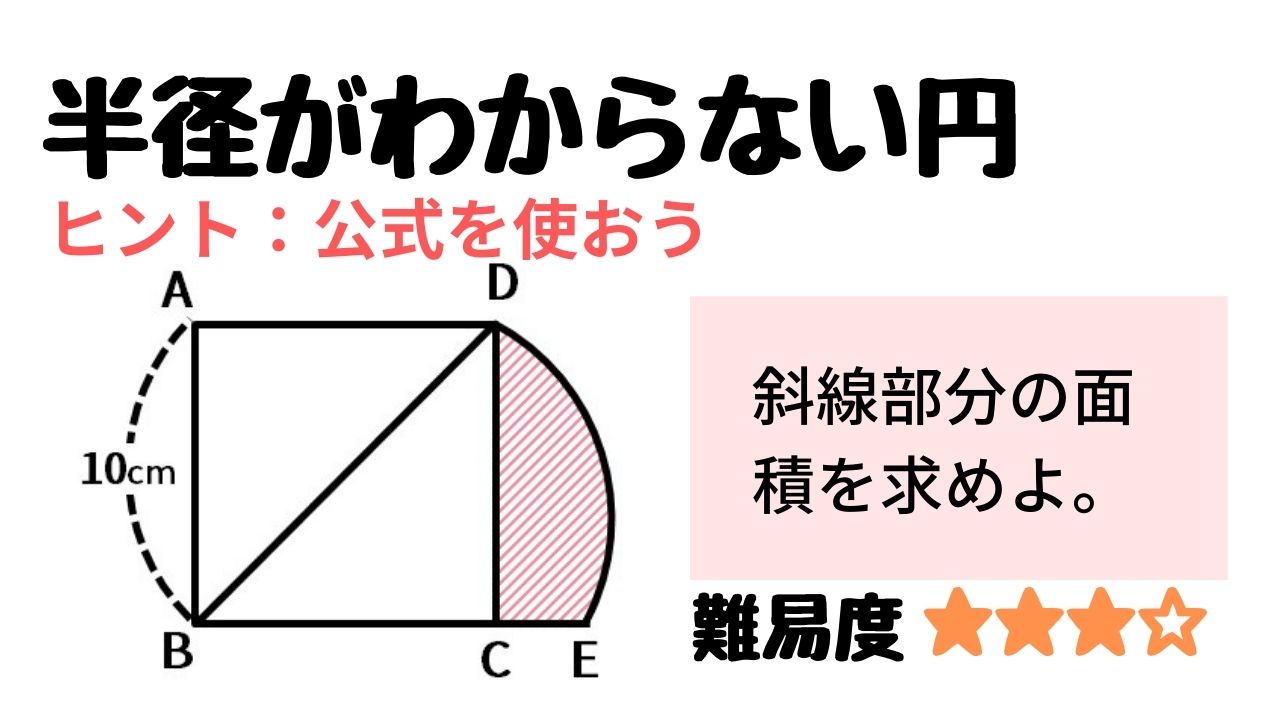 |  |
 |  | |
 |  |  |
 |  |  |
「円 面積 積分 一部」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  | |
「円 面積 積分 一部」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  |  |
 |  |  |
「円 面積 積分 一部」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  |  |
 |  |  |
「円 面積 積分 一部」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  | |
 |  | |
「円 面積 積分 一部」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
 | ||
「円 面積 積分 一部」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 | ||
 |  | |
「円 面積 積分 一部」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |
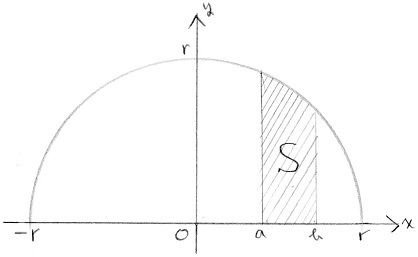
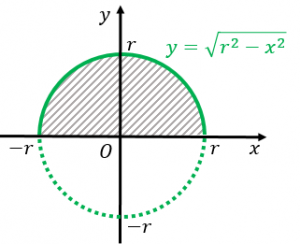
Web円の面積を2重積分で求める I = ∬ D d x d y, D x 2 y 2 ≤ 1 I = ∬ D d x d y は領域 D の面積を表すのであった。 D x 2 y 2 ≤ 1 つまり,領域 D は半径 1 の円の内部の面積であるから,Web覚えておくべき積分公式を整理しました。 いずれも積分後の式を微分することで確かめられます。 微分については 微分公式一覧(基礎から発展まで) をどうぞ。 目次 基本的な関数の
Incoming Term: 円 面積 積分, 円 面積 積分 一部, 円 面積 積分 極座標, 円 重なり 面積 積分, 円 直線 面積 積分,




0 件のコメント:
コメントを投稿